今日の活動
出来るようになってきた!
じゃんぷに来ている中学生のG君。通所したら必ずローマ字の「聴覚法」に取り組んでいます。
学習に対する苦手感が強い子なので,あまり「学習!」という雰囲気は出さずに本人の興味のあることを調べさせることでタイピングの練習をしています。
ローマ字表を見ながらキーボードを打っていますが,タイピングが上手になってきています。「む…『M』ってどこやー!」と言いながら打っているのですが…つまり「む」を打つ時は「MU」ということはもう覚えているのです。キーボードの並びを覚えることも苦手なので,アルファベットを探しているようです。
そういったこともあるので本人は「まだローマ字打てへん!覚えてない!」と感じているようですが,実はもう覚えているのです。毎回の聴覚法も「はいはい」と言いながら当然のように言っています。
今は「友達にWordで手紙を書く。」という取り組みをしようかなと話しています。苦手感があることに対して拒否感を示していたG君ですが,「全然いいよ。やろうや。」と乗ってきました。「出来るって感じてるやん!」と言うと「そんなことないわ!」と返してきますが,拒否はしません。本人自身も効果を感じてきているようです。
嘘のある遊び
『犯人は踊る』(犯人は誰?(「犯人は踊る」)(2022/6/26)で紹介したゲーム)が気に入ったE君。F君と遊ぶときに、『犯人は踊る』をリクエストしてきました。職員はそこで、「同じようなゲームでこんなのがあるんだけど」と、『人狼ドッチ』というゲームを提案してみました。
オリジナルの人狼ゲームは、テレビでも取り上げられることがあるほど、有名な会話ゲームです。複数人のプレイヤーが村人となるのですが、その中に、人狼という悪い人が紛れています。人狼は毎晩一人ずつ村人を食べていき、放っておくと村人は全滅してしまいます。そこで村人は毎朝、誰が人狼を推理し、追放していきます。うまく人狼を追放できたらクリアですが、間違って本当は村人の人を追放してしまうと、どんどん村人が不利になっていくというゲームです。
『人狼ドッチ』は、この人狼ゲームを、3人という少ない人数でもできて、1ゲーム5分ほどで終わるようアレンジしたもの。その中でも会話をする時間はしっかりと取られており、そこでの駆け引きが勝負のカギになります。人狼になった人が大事なのは、自分が人狼だとばれないように「嘘」をつくことです。この「嘘」をつき通せるかどうか、そして村人はこの「嘘」を見抜けるかで、勝負が決まります。
ですが、この「嘘」というのがやっかいなもの。「嘘」をつけない子は少なくありません。実際にこのとき遊んだF君も、「嘘」が苦手。人狼の時は隠さないといけないのに、堂々と「僕は人狼です」と言い放ちました。案の定、ほかの人から人狼だと票が集まり、負けとなってしまいました。
『人狼ドッチ』は難しかったかなあ、と職員は反省します。ですが、「嘘」を全くつけないというのも困りもの。大人からすると、一見利点のように思えるかもしれませんが、子ども同士では遊びの幅を狭めてしまうこともあります。ルールがあって、この遊びの中なら「嘘」をついてもいいよという場面に、またチャレンジ出来たら、と思います。
お互いに助け合おう!
じゃんぷでは七夕祭りということで短冊に願い事を書いたり,笹飾りを作ったりしています。
子ども達からは「世界的に有名なゲームを作りたい!」という将来の夢や「習い事の大会(コンクール)をがんばりたい!」という身近な夢,更には「世界が平和になりますように」という最近のニュースを知ってか知らずか,壮大な夢を書く子もいたりと,様々な願い事が見れます。
さて,願い事を書いている時にある子どもが「これってどういう字やったっけー?」と悩んでいると隣の子が「こう書くんやで」と優しく教えてくれる場面がありました。また,短冊を結ぶときに「ここやったら結びやすいで!」とアドバイスした子どもが今度は「こう結んだらいいんやで」とアドバイスを受けている場面も見られました。
また,折り紙手裏剣を作っている時に1年生の子が「こういう風に折ったらいいよ!先生綺麗に折れるからここまでやってくれたあとは僕が作っとくわ!」と言ってくれたこともありました。
それぞれの強みを生かしながら,お互いに助け合う姿が多く見られました。今回はこちらが何か仕掛けた訳ではなく,自然と生まれた子ども同士の関わり合いですが,ほっこりしたので紹介します。
漢字の「仕組み」を教える
漢字を覚える時,それぞれの漢字を一つずつ,漢字そのものを覚えようとするのは難しいです。以前も書いたように特に読み書きが苦手な子どもにとって,繰り返し練習は作業感が出てしまい苦手意識が強くなってしまうことがあります。
ただでさえ漢字は膨大な量があります。我々にとっても大変だったはずですが,しかしなんとか覚えることが出来ているのは何故でしょう?
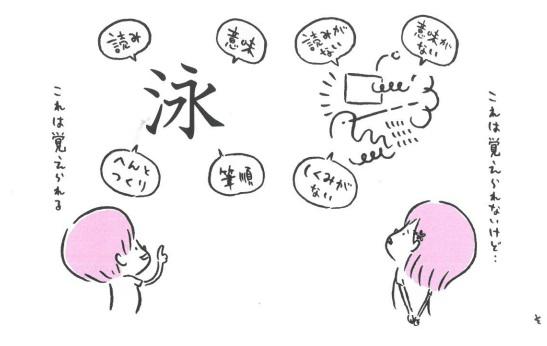
それは無意識のうちに「漢字の仕組み」を使っているからです。例えば,「泳」という漢字についてです。「さんずい」がついているから水に関係すること,そして「永」という部分があるから「エイ」という読みがありそうだ…というように,「へん」と「つくり」,あるいは意符と音符といった仕組みから漢字を理解し,覚えることが出来ます。
このように漢字の「仕組み」を教えると,漢字の「意味」を理解し,そこから読み,書きに繋がります。
「レストランに行ったよ!」
「なんで歩かなあかんの?」(2022/6/28)で紹介したAさん。梅雨で天気がぐずつく中、雨の降らない間をねらって歩行練習に精を出しました。外食の目標にしているファミリーレストランにも、練習で入口まで行ってみました。白杖でさくさく歩きますが、広い歩道では左に傾く癖があります。すぐそばで見守る職員が、癖が出たら指摘するようにして、歩行練習を重ねました。
さあ、いよいよ外食の日。当日は幸いなことに、雨の心配はなさそうな曇り空です。Aさんも出発する前から、「カルボナーラ食べたい」「シーフードピザ食べたい」と楽しみな様子。事前にメニューを職員が読んでいっしょに確認してから出発しました。歩行練習の甲斐があって、スムーズに歩くAさん。そばで見守る職員が手助けすることなく、ファミリーレストランに到着しました。
レストランに到着すると、店員さんもやさしく対応してくれました。まずAさんのために、点字のメニューを出してくれました。Aさんは点字を読んで、料理名と値段も一緒に確認していきます。シーフードピザがないことがわかると、すぐに「じゃあソーセージピザにする」と決定。店員さんを呼んで、注文します。「ジュースもありますか?」とAさんが聞くと、店員さんは「ドリンクバーがあります」と答えます。Aさんはすぐに「(ドリンクバーに)マスカットジュースはありますか?」と尋ねます。すると店員さんもすぐに「Qooって知っていますか?そのマスカットジュースがあります」と丁寧に答えてくれました。
注文の料理が届くまで、ドリンクバーにジュースを取りに行ったり、点字のメニューを見たりして過ごしたAさん。
「これ(点字メニュー)があるので、何があるのかよくわかって嬉しいです。良い思い出になりました。ありがとうございました。」
と料理を運んできてくれた店員さんにお礼を言ってメニューを返していました。楽しみだったソーセージピザも、せっかくの機会だからと職員に続いて、Aさんも自分でピザカッターを使って切ってみます。外食を満喫できた帰りもまた、白杖を使って自分で歩いて帰りました。
今年は異例な速さでの梅雨明けになりましたね。梅雨が明けて1週間は、夏を思わせるほどの暑さが続き、すてっぷでも屋根のない場所への外出は控えました。今は戻り梅雨のようで、すこし暑さがましになったので、曇り空の下、公園へ。外出の楽しみがあると、やはりモチベーションは上がります。夏休みも、もうすぐ。また外出の計画を立てて、お知らせしていきます。